[논문리뷰] Mamba: Linear-Time Sequence Modeling with Selective State Spaces

1. Transformer의 한계점

Transformer

Transformer는 긴 시퀀스 처리에 있어 효율이 나쁨

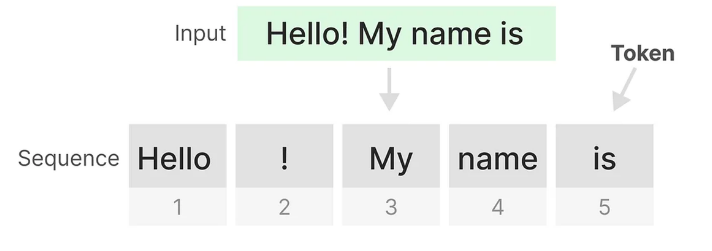
• Transformer의 장점은 이전 토큰을 돌아볼 수 있는 것
• 훈련 시 Multi-head masked self-attention 으로 각 토큰 별 병렬 처리를 함

• 토큰 별로 행렬을 만들어서 계산함

⇒ 병렬 처리를 통해 훈련 속도를 크게 높일 수 있음

• 추론 시, 전체 시퀀스에 대한 어텐션을 다시 계산해야 함
• 길이가 $L$인 시퀀스는 총 $L^2$의 계산이 필요함

즉, Training은 병렬 처리를 활용하여 빠르지만, Inference는 느림

 

RNN?

RNN은 시간 단계 t의 입력과 이전 시간 단계 t-1의 숨겨진 상태로, 다음 숨겨진 상태를 생성하고 출력을 예측함

• 이전 단계의 정보만을 다음 단계로 전달할 수 있음
• RNN은 시퀀스 길이와 선형적으로 비례하는 빠른 추론이 가능함

⇒ Why? 이전 상태만을 고려하기 때문

 

즉, Training은 병렬 처리가 불가능하여 순차적으로 단계를 거쳐 느림, Inference는 빠름

그렇다면 Transformer처럼 Training은 병렬화하여 빠르지만, RNN처럼 Inference를 선형적으로 하는 아키텍처는 없을까?

⇒ Mamba

 

2. State Space Model (상태 공간 모델)

• 상태 공간 : 어떤 시스템이나 프로세스의 모든 가능한 상태를 정의하고, 그 상태 간의 전이를 수학적으로 표현하는 방법
  • 간단하게 말해, 시스템의 가능한 모든 상태들을 포함하는 공간 
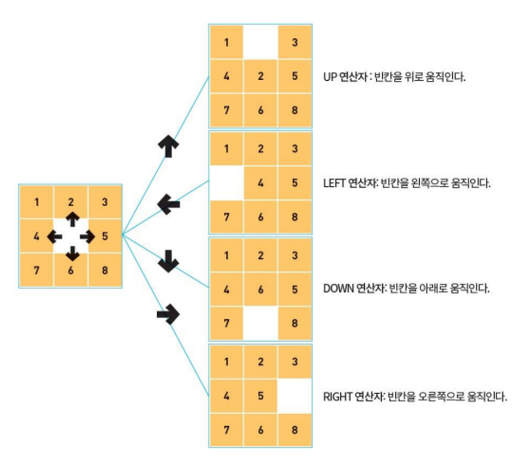
    • ex) 미로 탐험
      • 상태 : 미로 내의 위치
      • 상태 벡터 : 미로에서의 위치를 설명하는 변수
      • 상태 전이 : 현재 위치에서 다른 위치로 이동하는 과정

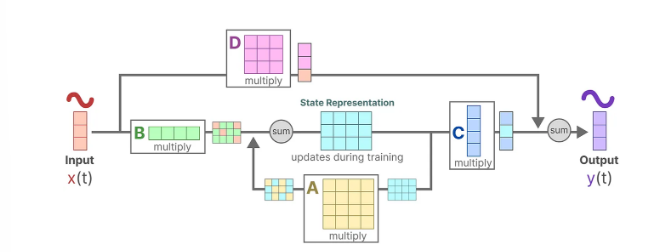
상태 공간 모델

SSM은 상태 표현을 설명하고 입력에 따라 다음 상태가 어떻게 될지 예측하는 모델

상태 공간 모델은 2 가지 기본 방정식으로 표현됨

상태 방정식 (State Equation)

• $h(t)$ : 현재 시스템의 상태 벡터 (현재 위치나 출구까지의 거리와 같은 정보)
• $A$ : 상태 전이 행렬. 시스템의 현재 상태가 다음 상태로 어떻게 전이되는지 나타냄
• $B$ : 입력 행렬. 입력 $x(t)$가 시스템에 미치는 영향을 나타냄
• $x(t)$ : 현재 시간 $t$에서 주어진 입력 (로봇이 미로에서 왼쪽으로 이동, 아래로 이동하는 지시)

$$ h(t+1)=Ah(t)+Bx(t) $$

 

현재 상태는 이전 상태와 현재 입력에 의해 업데이트됨 = 신경망의 hidden state가 새로운 입력을 받아 업데이트되는 것

• 출력 방정식 (Output Equation)
  • $C$ : 출력 행렬. 현재 상태 $h(t)$가 출력 $y(t)$에 어떻게 영향을 미치는지 나타냄
  • $y(t)$ : 출력 시퀀스. 모델이 예측하는 출력 (출구로 더 빨리 가기 위해 다음에 왼쪽으로 이동하는 것이 좋다는 결론 도출)
  • $D$ : 입력이 직접적으로 출력에 미치는 영향 (생략 가능 = Skip connection)

$$ y(t)=Ch(t) +Dx(t) $$

현재 상태가 시스템의 출력을 결정한다는 것

• 목적은 입력에서 출력 시퀀스로 이동할 수 있도록 이 상태 표현 $h(t)$를 찾는 것
• 입력 $x(t)$는 먼저 상태를 업데이트합니다. (상태 방정식)
• 그런 다음, 이 업데이트된 상태를 통해 출력을 계산합니다. (출력 방정식)

예를 들어, 내비게이션 시스템으로 생각

• 상태 방정식 : 현재 위치에서 다음 위치로 이동할 때의 경로를 계산. 현재 위치(상태)는 이전 위치와 새로운 입력(방향 지시)에 따라 업데이트
• 출력 방정식 : 새롭게 계산된 위치를 기반으로, 목적지까지 얼마나 남았는지 또는 다음 방향이 어디인지 출력

• 입력이 연속적으로 예상되므로 SSM의 주요 표현은 연속 시간 표현
  • SSM이 다루는 시스템이 시간의 모든 순간에 연속적으로 입력을 받아야 하는 상황

연속 시간(Continuous-Time) vs. 이산 시간(Discrete-Time)

• 연속 시간 : 끊김 없이 연속적으로 흐름. 즉, 시간의 모든 순간을 고려함
• 이산 시간 : 시간이 일정한 간격으로 나뉘어 있음.

왜 연속적인 입력이 중요한가? 일반적으로 현실 세계의 많은 시스템은 연속 시간으로 동작 상태 공간 모델에서는 시스템의 상태가 시간에 따라 어떻게 변하는지 추적

• 만약 입력이 연속적으로 변하는 경우(예: 지속적으로 바뀌는 속도나 온도), 모델은 시간의 모든 순간에 대해 상태를 업데이트해야 함 > 연속 시간 표헌

텍스트 시퀀스는 이산적

• 실수인가? no
• 단어, 문자, 토큰과 같은 개별적인 단위로 구성되어 있음
• 무한히 세밀하게 쪼갤 수 없는 불연속적인 값

"The quick brown fox.” ⇒ “The” 와 “quick” 사이에 무한한 중간 값이 존재하는가?

제로-오더 홀드 (zero-order hold)

우리는 일반적으로 이산 입력(텍스트 시퀀스)를 가지고 있기 때문에, 모델을 이산화해야함

제로-오더 홀드

• 이산 신호를 받으면 새로운 이산 신호를 받을 때까지 그 값을 유지

⇒ SSM이 사용할 수 있는 연속 신호를 생성

재귀적 표현

RNN과 비슷하게 이전 상태와 현재 입력을 사용해 다음 상태를 계산하고, 그 상태를 통해 출력을 생성함

왜 중요한가? 빠른 추론이 가능함

컨볼루션 표현

CNN에서 사용하는 커널을 적용한 집합적 특징 도출

 

• 텍스트를 다루고 있기에 1차원 관점 필요

• $y$ : output
• $x$ : input
• $k$ : kernel

• 일관된 시퀀스 길이를 유지하기 위해서 문장의 끝에 패딩을 적용

연속적, 재귀적, 컨볼루션

• 재귀적 SSM을 통해 Inference와 컨볼루셔널 SSM을 통해 병렬화된 훈련이 가능함

선형 시간 불변성(Linear Time Invariance, LTI)

• SSM의 매개변수인 A,B,C가 모든 시간 단계에 대해 고정
• 즉, 시스템의 동작이 시간이 지나도 변하지 않으며, 이는 정적 표현

A matrix

이전 상태에 대한 정보를 포착하여 새로운 상태를 구축

• 상태 전이 방정식에서 행렬 A는 상태의 변화를 정의
• 시스템의 장기적 의존성을 모델링하는 데 핵심적
• 행렬 A를 설계하는 방법에 따라, 모델이 얼마나 많은 과거 정보를 기억할 수 있는지가 결정

HiPPO (Hungry Hungry Hippo)

• 장기 메모리를 관리하기 위한 방법
• 최근의 입력이 중요, 오래된 입력은 덜 중요 > 이를 고려하여 행렬 A를 설계

Structured State Space for Sequences (S4)

• S4는 HiPPO를 사용하여 상태 공간 모델 (SSM)을 개선한 것
• 시퀀스 데이터를 처리하는 데 효과적이며, 재귀적 또는 컨볼루셔널 표현을 통해 장거리 의존성을 효율적으로 처리

3. Selective State Space Models - Mamba

해결할 문제

Selective Copying (선택적 복사)

• SSM은 Copying task를 수정하여 토큰의 위치를 변경
• 중요한 토큰은 기억하고 불필요한 토큰을 필터링하는 내용 인식(content-aware) 추론이 필요

⇒ LTI 기반인 SSM은 내용 인식 추론 X

⇒ A,B,C 행렬은 각 토큰을 동등하게 여김

Induction Heads (유도 헤드)

• 적절한 문맥에서 올바른 출력을 생성하는 데 필요한 내용 인식 추론을 요구
• 이전에 발견한 패턴을 추출해서 재현하는 것

⇒ LTI 기반인 SSM은 이전 토큰 중 어떤 것을 기억할지 선택할 수 없음

반면? Transformer라면??

• 입력 시퀀스에 따라서 동적으로 어텐션을 변경할 수 있음

즉, SSM이 이러한 작업에서 성능이 떨어지는 것은 시간 불변성 SSM의 근본적인 문제, A,B,C 행렬의 정적인 특성으로 인한 내용 인식 문제를 시사함

따라서 시퀀스 모델을 구축하는 기본 원리는 선택성(selectivity), 순차적 상태에서 입력을 선택하거나 필터링할 수 있는 능력

Improving SSMs with Selection (S6 구조를 제안)

• 기존 S4 $(D,N)$ → S6 $(B,L,N)$
  • $B$ : 배치 크기 (배치마다 시퀀스 길이 $L$에 맞춰 파라미터 조정)
  • $L$ : 시퀀스 길이
  • $N$ : 새로운 숨겨진 차원

• 기존에 고정시켜 놓았던 SSM의 파라미터인 B,C, Step size(*∆)*를 학습 가능한 파라미터로 만들어 시퀀스 사이의 관계에 영향을 주도록 함
• 기존에는 고정된 A,B,C로 연산 (LTI) ⇒ 모든 토큰에 동등한 역할 수행
• 상태 매트릭스 $A$ 고정, 제어 매트릭스 $B$와 출력 매트릭스 $C$는 입력에 따라 동적으로 변함 ⇒ 각 입력에 대한 동적인 영향을 모델링 가능
• discretization parameter Δ를 조절하여 각 입력에 따라 서로 다른 step을 주어 적절하게 토큰의 관계를 해석

즉, 파라미터 shape을 조절해서 Time-varying으로 변화해줘 동적으로 모델링 가능하도록 함

Overview of Selective Scan

동적인 커널을 사용하며 convolution과 같이 고정된 커널 $B,C$를 활용하지 못하게 됨

• 컨볼루션의 병렬화 x / 재귀적 표현 o

재귀적 표현과 스캔 작업

각 상태는 이전 상태와 현재 입력의 합 > 스캔 작업

$h_t = A \times h_{t-1} + B \times x_t$

• $h_t$ : 현재 상태 / $h_{t-1}$ : 이전 상태
• for 루프를 사용해 처리할 수 있지만 병렬화는 어려움

⇒ 이전 단계의 결과가 없으면 다음 단계를 계산할 수 없기 때문

 

병렬 스캔 알고리즘의 사용

계산 순서에 구애받지 않고, 데이터를 부분적으로 계산하고 나중에 합치는 방식

1. 부분 상태 계산 : 시퀀스를 여러 부분으로 나누고, 각 부분에서 상태 계산을 병렬로 수행 (계산 순서에 크게 의존하지 않기 때문에 병렬 처리 가능)
2. 결합 단계 : 나누어 계산한 부분 결과를 다시 합쳐 전체 시퀀스의 상태 계산

하드웨어 인식 알고리즘

GPU는 고속의 SRAM(작지만 빠름)과 저속의 DRAM(크지만 느림)이라는 두 가지 메모리를 사용함. 두 메모리 간의 데이터를 자주 이동하는 것이 작업을 느리게 만드는 주요 원인

⇒ 커널 융합 (Kernel Fusion)

• 작업을 한 번에 모아서 처리하고, 중간 결과를 메모리에 저장하지 않도록 함

• 스텝 크기 / 선택적 스캔 알고리즘 / C와의 곱셈 ⇒ 하나의 커널로 융합

4. Mamba Architecture

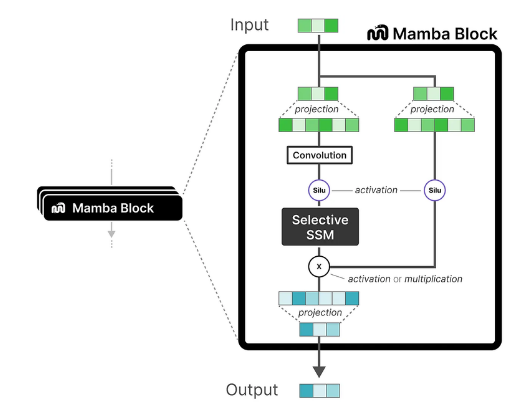
맘바 블록의 주요 구성 요소

1. Linear Projection
2. Convolution
3. Selective SSM

Selective SSM의 역할

• 이산화 (Discretization): 연속적인 데이터를 이산 데이터로 변환하여 처리
• HiPPO 초기화: 장거리 의존성을 효과적으로 포착하기 위해 행렬 A를 특수하게 초기화
• 선택적 스캔 알고리즘: 병렬 처리를 통해 연산을 효율적으로 수행하면서 중요한 정보를 선택적으로 강조
• 하드웨어 인식 알고리즘: 최신 하드웨어(GPU 등)의 성능을 극대화하기 위해 설계된 알고리즘

최종 출력

맘바 블록은 정규화 레이어와 소프트맥스 함수를 통해 최종 출력을 생성

최종적으로 선택된 출력 토큰이 모델의 예측 결과가 됨

 

결론

맘바는 SSM을 사용하여 효율적이고 강력한 정보 처리를 가능하게 함. 특히 장기적인 의존성을 포착하고 하드웨어 성능을 최대한 활용할 수 있도록 설계됨. 특히 빠른 추론과 훈련, 그리고 더 넓은 맥락을 고려하는 작업에서 강력한 성능을 발휘할 것으로 기대됨.