[논문리뷰] Diffusion 논문 수식 정리

https://www.youtube.com/watch?v=ybvJbvllgJk

https://youtu.be/uFoGaIVHfoE?si=eRGixNZxxetAPi_1

 

diffusion loss 정리

1. Forward Diffusion Process 
   • 원본 데이터(이미지)에 점진적으로 가우시안 노이즈를 추가하는 과정
   • noisy해지는 process (Forward diffusion process)
     $$q(x_t | x_{t-1}) = \mathcal{N}(x_t; \sqrt{1 - \beta_t} x_{t-1}, \beta_t I)$$
   • 단계가 진행될수록 데이터가 점점 더 노이즈로 변하며, 최종적으로는 순수한 가우시안 노이즈가 됨
2. Reverse Denoising Process
   • 학습된 신경망(Neural Network)을 사용하여 노이즈에서 점진적으로 원본 이미지를 복원하는 과정
   • noisy를 걷어내는 process (Reverse denoising process)
     $$p_\theta(x_{t-1} | x_t) = \mathcal{N}(x_{t-1}; \mu_\theta(x_t, t), \sigma_t^2 I)$$
   • 평균(μ)과 분산(σ)을 이용하여 역으로 노이즈를 제거하며, 네트워크가 이를 학습
3. 손실 함수 (Loss Function)
   • 네트워크는 원본 데이터의 노이즈 분포를 예측하는 방식으로 학습

$$L_{\text{simple}} = \mathbb{E}_{x_0 \sim q(x_0), \epsilon \sim \mathcal{N}(0, I), t \sim U(1, T)} ||\epsilon - \epsilon_\theta (\sqrt{\bar{\alpha}_t} x_0 + \sqrt{1 - \bar{\alpha}_t} \epsilon, t)||^2$$

1. • 즉, 네트워크가 주어진 노이즈를 얼마나 잘 예측하는지를 측정하는 방식

 

 

1) Bayesian Rule (베이즈 정리)

베이즈 정리는 확률 변수를 조건부 확률로 변환하는 공식이다.

$$p(A|B) = \frac{p(B|A) p(A)}{p(B)}$$

이것을 diffusion 모델에서 적용하면 다음과 같은 형태로 사용된다.

$$q(x_{t-1} | x_t, x_0) = \frac{q(x_t | x_{t-1}, x_0) q(x_{t-1} | x_0)}{q(x_t | x_0)}$$

 

2) Markov Chain (마르코프 성질)

마르코프 성질은 현재 상태가 주어졌을 때, 이전 상태에 대한 조건부 확률이 독립임을 의미한다.

$$q(x_t | x_{t-1}, x_{t-2}, ..., x_0) = q(x_t | x_{t-1})$$

즉, 과거 모든 정보가 아니라 직전 상태만으로 현재 상태가 결정된다는 성질을 가지고 있다.

 

(17) → (18)

$$L = E_q \left[ -\log p(x_{0:T}) + \sum_{t \geq 1} \log \frac{p_\theta(x_{t-1} | x_t)}{q(x_t | x_{t-1})} \right]$$

(19) → (20)

markov chain로 인해 해당 식이 성립한다.

$$\begin{gather} q ( x _ { t } | x _ { t - 1 } ) \\ = q ( x _ { t } | x _ { t - 1 } , x _ { 0 } ) \end{gather}$$

bayesian rule로 인해서 

$$q ( x _ { t } | x _ { t - 1 } , x _ { 0 } ) = \frac { q ( x _ { t } , x _ { t - 1 } , x _ { 0 } ) } { q ( x _ { t - 1 } , x _ { 0 } ) } $$

로 표현할 수 있다. 

$$ = \frac { q ( x _ { t } , x _ { t - 1 } , x _ { 0 } ) } { q ( x _ { t - 1 } , x _ { 0 } ) } \cdot \frac { q ( x _ { t } , x _ { 0 } ) } { q ( x _ { t } , x _ { 0 } ) }$$

 

다시 bayesian rule로 인해서

$$q ( x _ { t - 1 } | x _ { t } , x _ { 0 } ) \cdot \frac { q ( x _ { t } , x _ { 0 } ) } { q ( x _ { t - 1 } , x _ { 0 } ) }$$

로 정리된다. 

 

(20) → (21)

$$- \sum _ { t > 1 } \log \frac { p _ { \theta } ( x _ { t - 1 } | x _ { t } ) } { q ( x _ { t - 1 } | x _ { t } , x _ { 0 } ) } \cdot \frac { q ( x _ { t - 1 } | x _ { 0 } ) } { q ( x_t | x _ { 0 } ) }$$

에서 log의 성질을 이용하여 

$$- \sum _ { t > 1 } \log \frac { p _ { \theta } ( x _ { t - 1 } | x _ { t } ) } { q ( x _ { t - 1 } | x _ { t } , x _ { 0 } ) } - \sum _ { t > 1 } \log \frac { q ( x _ { t - 1 } | x _ { 0 } ) } { q ( x _ { t  } | x _ { 0 } ) }$$

으로 변환한다.

 

이때 $\sum _ { t > 1 } \log \frac { q ( x _ { t - 1 } | x _ { 0 } ) } { q ( x _ { t  } | x _ { 0 } ) }$을 전개하면 아래 식이 된다. 

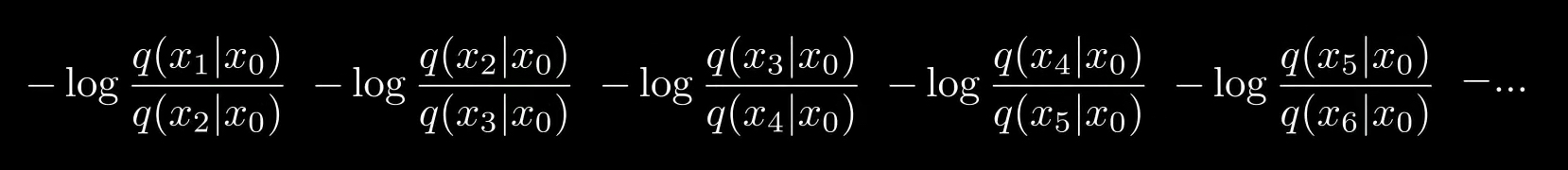
식을 정리해주면

$$- \log \frac { q ( x _ { 1 } | x _ { 0 } ) } { q ( x _ { T } | x _ { 0 } ) }$$

가 된다.

 

(20)번 식에서 $q(x_1 | x_0)$을 정리하고 $\log {p_{ \theta} (x_0 | x_1)}$ 는 뒤에 남겨두고 $\log \frac {1} { q ( x _ { T } | x _ { 0 } ) }$는 식 앞으로 정리해서 (21)번 식을 만든다. 

 

diffusion 모델

Neural Network(예를 들어 UNet 기반 모델)는 입력으로 \( x_t \) (노이즈가 \( t \) 스텝만큼 추가된 이미지)를 받아서, \( x_{t-1} \)을 복원하도록 학습한다. 

• 입력: \( x_t \) (데이터 \( x_0 \) 에게 \( t \) 단계의 노이즈를 추가한 결과)
• 출력: \( x_{t-1} \) (데이터 \( x_0 \) 에게 \( t-1 \) 단계의 노이즈를 추가한 결과와 같도록)

이때 Neural Network는 \( x_t \)에서 제거해야 하는 노이즈 \( \epsilon \)을 예측한다. 즉, $t$에서 $t-1$로 갈 noise를 걷어내는 과정이다.